机器学习：分类算法(1)逻辑回归

算法原理

Logistic回归与多元线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalized linear model）。

这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

• 如果因变量是连续的，就是多元线性回归；
• 如果是二项分布，就是Logistic回归；
• 如果是Poisson分布（$P(X=x)=\frac{m^x}{x!}e^{-m}$，平均为m时取值为x的概率），就是Poisson回归；
• 如果是负二项分布，就是负二项回归。

Logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类的Logistic回归。

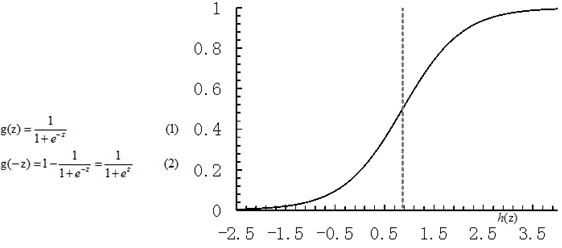
逻辑回归其实是在线性回归的基础上，加上一层逻辑函数 Sigmoid 映射，将预测值限定为(0,1)间。

Sigmoid 函数连续可微分。在z=0时，十分敏感，在z>>0或z<<0处，都不敏感。

公式推导

逻辑回归定义

假设样本数目为m，样本特征维度为n，$x$的形状为(m, n)，$y$的形状为(m,)，$y$的取值为0或者1。

对应的，$w$的形状为(n, 1)，$b$形状为(1,1)。

逻辑回归的初始抽象为下式，对于$x^{(i)}$的每个特征$x_j^{(i)}$，求解一个权重$w_j$，以及一个常数项（截距）$b$，使得经过Sigmoid变换得到的加权预测值与真实值尽可能相等。

$$y=\sigma (w^Tx+b)$$ $$\sigma(z) = \frac{1}{1+e^{-z}}$$

通过将$w$和$b$合并为$\theta$，再将以上两个式子代入，有：

$$y=\sigma(\theta^Tx)=\frac{1}{1+e^{-\theta ^ T x}}$$

该预测函数表示分类结果为1时的概率。因此对于输入点x，分类结果为类别1和类别0的概率分别为如下公式：

$$p(y=1|x;\theta)=h_{\theta}(x)$$ $$p(y=0|x;\theta)=1-h_{\theta}(x)$$

损失函数

对于一组数据集，样本数据x={x1, x2, … , xm}对应的观测值为y={y1, y2, … , ym}。那么可以知道样本{x1, x2, … , xm}取到观测值{y1,y2,...,ym}的概率为:

$$L(\theta)=L(y_1,y_2,...,y_m;\theta)=\prod_{i=1}^{m}p(y_i;\theta)$$

这一概率随 $\theta$的取值而变化，它是 $\theta$的函数，称 $L(\theta)$为样本的似然函数。

而某个样本 $x_i$取值为 $y_i$的后验概率如下形式：

$$p(y_i|x_i;\theta)=(h_\theta(x_i))^{y_i}·(1-(h_\theta(x_i)))^{1-y_i}$$

假设分类器分类足够准确，此时对于一个样本，如果它是属于1类，分类器求出的属于1类的概率应该尽可能大，即$p(y=1lx)$尽可能接近1；如果它是0类，分类器求出的属于0类的概率应该尽可能大，即$p(y=0lx)$尽可能接近1。通过上述公式对二类分类的情况分析，可知我们的目的是求取参数 $\theta $，使得 $L(\theta) $对观测值的分类结果尽可能取最大值。

对其取对数，可得到以下公式，即我们要求取 $\theta $，使得下式在样本数据上取值最大：

$$l(\theta)=log(L(\theta))=\sum_{i=1}^m(y_ilog(h_\theta(x_i)) + (1-y_i)log(1-h_\theta(x_i)))$$

然而实际上我们定义的损失函数是求最小值，于是，很自然的，我们想到对式子加一个负号，再取平均值，就变成了求最小值的问题，这就得到了逻辑回归中的损失函数，优化使其最小：

$$J(x;\theta) = -\frac{1}{m}\sum_{i=1}^{m}(y_ilog(h_\theta(x_i)) + (1-y_i)log(1-h_\theta(x_i)))$$

定义 $y’=h_{\theta}(x)$，那么以上式子简化为

$$J=-(y\mathrm {log} y' + (1-y)\mathrm{log}(1-y'))$$

梯度下降

对应参数$\theta_j$的求导为：

$$\begin{equation}\begin{split}\frac{\partial J}{\partial \theta_j} &=-(\frac{y}{y'}-\frac{1-y}{1-y'})\times \frac{\partial y'}{\partial \theta_j} \\ &=-(\frac{y}{y'}-\frac{1-y}{1-y'})\times\frac{\partial \sigma(\theta ^ Tx)}{\theta_j} \\ &=-(\frac{y}{y'}-\frac{1-y}{1-y'})\times \sigma(\theta^Tx)(1-\sigma(\theta^Tx))\times \frac{\partial \theta^Tx}{\partial \theta_j}\\ &= -(\frac{y}{y'}-\frac{1-y}{1-y'})\times y'(1-y')x_j\\ &=-(y(1-y')-(1-y)y')x_j\\ &=(y'-y)x_j \end{split}\end{equation}$$

第三步用到了Sigmoid函数的求导：

$$\frac{\partial \sigma}{\partial z} = \sigma(z)(1-\sigma(z))$$

第五步是通分再化简。

最后通过梯度下降，更新参数 $\theta $：

$$\theta_j = \theta_j - \alpha(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$

拓展

场景回归具有计算代价低、速度快、容易理解和实现的优点，但同时容易欠拟合、分类和回归的精度不高；其常采用AUC来评估。

多元逻辑回归

二元逻辑回归可以一般化为多元逻辑回归用来训练和预测多分类问题。对于多分类问题，算法将会训练出一个多元逻辑回归模型， 它包含K-1个二元回归模型。给定一个数据点，K-1个模型都会运行，概率最大的类别将会被选为预测类别。具体可以参考逻辑回归基础

逻辑回归和SVM

SVM的损失函数为： $ J=\frac{1}{m}\sum_{i=1}^{m}(1-y_i[w_0+x_i^Tw_1])^++\lambda||w_1||/2 $

LR的损失函数为： $J=\frac{1}{m}\sum_{i=1}^{m}-log(g(y_i[w_0+x_i^Tw_1])+\lambda||w_1||/2) $

其中 $g(z) $为 $sigmoid $函数。

将两者统一起来，即 $J=\frac{1}{m}\sum_{i=1}^{m}Loss(y_i[w_0+x_i^Tw1]) + \lambda||w_1||/2 $

也就是说，他们得主要区别是逻辑回归采用得是log loss，而svm采用得是hinge loss即 $E(z) = max(0, 1-z) $

SVM损失函数为 $Loss(z)=(1-z)^+ $

LR损失函数为 $Loss(z)=log(1+e^{-z}) $

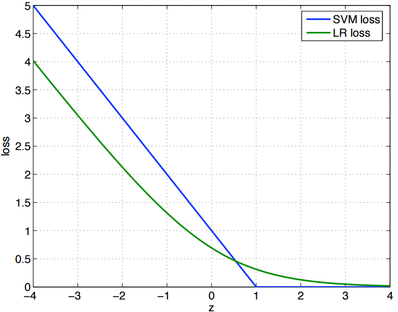
其实，这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。

SVM的处理方法是只考虑 support vectors，也就是和分类最相关的少数点，去学习分类器。

而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重，两者的根本目的都是一样的。

Python 实现

# -*- utf-8 -*-
# source: https://github.com/liuph0119/KnowledgeCloud/blob/master/Code/python/algorithms/MachineLearning/linear_models/logistic_regression.py

import numpy as np
from Code.python.algorithms.MachineLearning.utils.utils import mini_batches, log_msg
from Code.python.algorithms.MachineLearning.metrics.losses import neg_log_loss, neg_log_loss_grad, \
    l1norm_loss, l1norm_loss_grad, l2norm_loss, l2norm_loss_grad
from Code.python.algorithms.MachineLearning.metrics.scores import accuracy
from Code.python.algorithms.MachineLearning.utils.preprocess import Standardization
from sklearn.datasets.samples_generator import make_classification
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split


class LogisticRegression:
    def __init__(self, penalty='l2', alpha=0.01, fit_intercept=True):
        """ initialize model parameters.
        :param penalty: string, default 'l2'.
            regularization functions.
        :param alpha: float, default 0.01.
            regularization parameter.
        :param fit_intercept: bool, default True.
            whether to fit intercept.
        """
        self.w = None
        self.coef_ = None
        self.intercept_ = None
        self.penalty = penalty
        self.alpha = alpha
        self.fit_intercept = fit_intercept

    def _sigmoid(self, x):
        """ sigmoid function
        :param x: array
        :return: array
        """
        return 1 / (1 + np.exp(-x))

    def fit(self, x, y, learning_rate=0.001, batch_size=256, n_epochs=100, verbose=2):
        """ fit model via mini-batch gradient descent
            y = xw
            loss = 1/2 * (y' - y) ^ 2 = 1/2 * (xw - y) ^ 2
            grad = (xw - y) * x.T
        :param x: array of shape '(n_sample, n_features)'.
            training features.
        :param y: array of shape '(n_samples, 1)'.
            training labels.
        :param learning_rate: float, default 1e-3.
            learning rate of gradient descent.
        :param batch_size: int, default 256.
            batch size.
        :param n_epochs: int, default 1000.
            number of training epochs.
        :param verbose: int, default 1.
            whether to print log, '1' for printing while '2' for not printing.
        :return: None.
        """
        n_samples, n_features = x.shape[0], x.shape[1]
        batch_size = n_samples if batch_size == -1 else batch_size
        if self.fit_intercept:
            x = np.c_[np.ones(n_samples), x]
            n_features += 1
        self.w = np.random.rand(n_features) * 0.001

        loss = np.inf
        for i in range(1, n_epochs + 1):
            data_iter, _ = mini_batches(x, batch_size, shuffle=True)
            _iter = 1
            for bc_idx in data_iter:
                bc_x, bc_y = x[bc_idx], y[bc_idx]
                bc_h = self._sigmoid(np.dot(bc_x, self.w))
                loss, grad = neg_log_loss(bc_y, bc_h), neg_log_loss_grad(bc_y, bc_h, bc_x)
                penalty_loss = l1norm_loss(self.w) if self.penalty == 'l1' else l2norm_loss(self.w)
                penalty_grad = l1norm_loss_grad(self.w) if self.penalty == 'l1' else l2norm_loss_grad(self.w)
                loss += self.alpha * penalty_loss
                grad += self.alpha * penalty_grad
                self.w = self.w - learning_rate * grad
                _iter += 1
                if verbose == 1:
                    log_msg('# epoch {} iter {}: loss={:.4f}'.format(i, _iter, loss))
            if verbose == 2:
                log_msg('# epoch {}: loss={:.4f}'.format(i, loss))

        if self.fit_intercept:
            self.coef_ = self.w[1:]
            self.intercept_ = self.w[0]

    def predict(self, x):
        n_samples = x.shape[0]
        if self.fit_intercept:
            x = np.c_[np.ones(n_samples), x]
        return self._sigmoid(np.dot(x, self.w))

    def evaluate(self, x, y):
        preds = self.predict(x)
        preds_cls = np.where(preds >= 0.5, 1, 0)
        return {
            'neg_log': neg_log_loss(y, preds),
            'accuracy': accuracy(y, preds_cls)
        }


if __name__ == '__main__':
    # x, y = make_classification(n_samples=1000, n_features=5, n_classes=2, random_state=0)
    dataset = load_breast_cancer()
    x, y = dataset.data, dataset.target
    x = Standardization().fit_transform(x)  # feature standardization
    train_x, val_x, train_y, val_y = train_test_split(x, y, train_size=0.8, random_state=0)
    lm = LogisticRegression(penalty='l2', alpha=0.0001, fit_intercept=True)
    lm.fit(train_x, train_y, batch_size=256, learning_rate=1e-1, n_epochs=1000, verbose=0)
    print(lm.evaluate(val_x, val_y))
    print(lm.coef_, lm.intercept_)

{'neg_log': 0.08890522978727333, 'accuracy': 0.9649122807017544}
[-0.45478431 -0.64234883 -0.44067522 -0.50760714 -0.29955039  0.24108883
 -0.67537672 -0.81173429 -0.34771395  0.33409457 -1.31182764 -0.01518276
 -0.95374527 -0.94939778  0.2999703   0.74118571  0.06980219 -0.19351303
  0.25084997  0.82447949 -0.93439331 -1.07183487 -0.82462772 -0.90376259
 -0.67492585 -0.12909415 -0.87817014 -1.04012189 -0.64792583 -0.38643453] 0.28201798017381163

Scikit-learn API

from sklearn.linear_model import LogisticRegression
    lr = LogisticRegression(fit_intercept=True)
    lr.fit(train_x, train_y)
    preds = lr.predict_proba(val_x)[:, 1]
    preds_cls = np.where(preds >= 0.5, 1, 0)
    metrics = {
        'neg_log': neg_log_loss(val_y, preds),
        'accuracy': accuracy(val_y, preds_cls)
    }
    print(metrics)

{'neg_log': 0.09145479629044562, 'accuracy': 0.9649122807017544}